Рекуррентные сети на базе персептрона

Содержание

Введение
Сеть RMLP
Рекуррентная сеть Эльмана

Введение

Рассматриваемые здесь рекуррентные сети представляют собой развитие однонаправленных персептронных сетей за счет внесения в них обратных связей от выходного или промежуточных слоев на вход. В каждой обратной связи присутствует элемент единичной задержки. За счет этого сеть может рассматриваться как однонаправленная, при этом задержанные сигналы обратной связи просто увеличивают размерность входного вектора. Тем не менее алгоритмы обучения таких сетей более сложны, чем алгоритмы обучения однонаправленных сетей.

Ниже рассматриваются два вида сетей данного типа.

Сеть RMLP

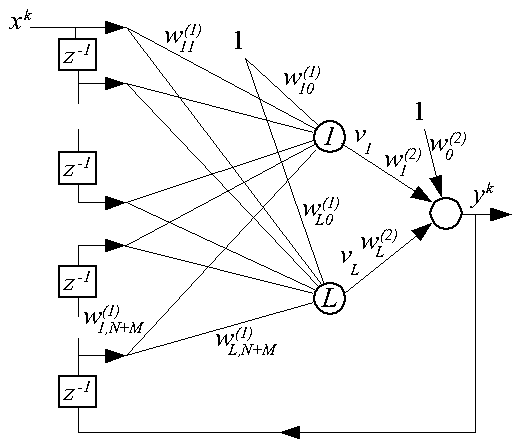
Данные сети получаются из однонаправленного многослойного персептрона MLP введением обратных связей с задержкой с выхода на вход сети, поэтому они получили название RMLP (Recurrent MultiLayer Perceptron). На рисунке дана структурная схема двухуровневой сети с одним входом, одним выходом и L нейронами в первом слое нейронов ("1-L-1").

Входной вектор сети имеет следующий вид:

[1,x^k,x^k-1, ...,x^k-(N-1),y^k-1,y^k-2, ...,y^k-M]^T, где(N-1) - количество задержек входного сигнала, M - количество задержек выходного сигнала.

Пусть все нейроны имеют сигмоидальную функцию активации. Тогда для каждого нейрона первого слоя

u_i=sum[j=0:N+M](w⁽¹⁾_ij*x_j), v_i=f(u_i),

а для единственного выходного нейрона

g=sum[i=0:L](w⁽²⁾_i*v_i)=sum[i=0:L](w⁽²⁾_i*f(u_i)), y=f(g).

Для обучения сети используется метод градиента, минимизирующий целевую функцию

E^k(W)=(1/2)*(y^k-d^k)².

Найдем компоненты градиента целевой функции сначала для выходного слоя

дE^k(W)/дw⁽²⁾_n = (y^k-d^k)*dy^k/dw⁽²⁾_n
= (y^k-d^k)*df(g^k)/dg^k*dg^k/dw⁽²⁾_n
= (y^k-d^k)*df(g^k)/dg^k*sum[i=0:L](d(w⁽²⁾_i*v^k_i)/dw⁽²⁾_n).

Ясно, что производная dw⁽²⁾_i/dw⁽²⁾_n равна 1 при n=i и равна 0 во всех остальных случаях. Поэтому

дE^k(W)/дw⁽²⁾_n = (y^k-d^k)*df(g^k)/dg^k*(v^k_n+sum[i=0:L](w⁽²⁾_i*dv^k_i/dw⁽²⁾_n)).

Причем

dv^k_i/dw⁽²⁾_n = df(u^k_i)/du^k_i*sum[j=0:N+M](w⁽¹⁾_ij*dx_j/dw⁽²⁾_n)
= df(u^k_i)/du^k_i*sum[j=1:M](w⁽¹⁾_i,N+j*dy^k-j/dw⁽²⁾_n)

поскольку первые N компонентов входного вектора от весов сети никак не зависят.

В итоге получаем довольно громоздкие рекуррентные выражения для расчета производной выходного сигнала по любому весу выходного нейрона в момент k по ее значениям в M предыдущих моментов k-1, k-2, ...,k-M.

dy^k/dw⁽²⁾_n = df(g^k)/dg^k*(v^k_n+sum[i=0:L](w⁽²⁾_i*df(u^k_i)/du^k_i*sum[j=1:M](w⁽¹⁾_i,N+j*dy^k-j/dw⁽²⁾_n))).

Для расчета производной в первые M моментов от начала обучения полагают

dy⁰/dw⁽²⁾_n = dy^-1/dw⁽²⁾_n = ... = dy^-M+1/dw⁽²⁾_n = 0.

Аналогичным образом получается выражение для производной выходного сигнала y^k по весу нейрона входного слоя w⁽¹⁾_nm

dy^k/dw⁽¹⁾_nm = df(g^k)/dg^k*sum[i=1:L](w⁽²⁾_i*df(u^k_i)/du^k_i*sum[j=1:L](w⁽¹⁾_i,N+j*dy^k-j/dw⁽²⁾_n)+deltha_in*x _m)), где deltha_in - дельта Кронекера. Напомним, deltha_in=1 тогда и только тогда, когда i=n, для всех остальных сочетаний i и n дельта Кронекера равна 0.

После получения выражений для производных алгоритм обучения сети RMLP можно сформулировать следующим образом.

Инициализировать все весовые коэффициенты сети, положить k=1.
Для текущего момента k рассчитать все сигналы сети.
Рассчитать значения dy^k/dw⁽²⁾_n и dy^k/dw⁽¹⁾_nm для всех взвешенных связей сети.
Уточнить все веса, используя формулы w⁽²⁾_n<-w⁽²⁾_n-nu*(y^k-d^k)*dy^k/dw⁽²⁾_n
и
w⁽¹⁾_nm<-w⁽¹⁾_nm-nu*(y^k-d^k)*dy^k/dw⁽¹⁾_nm, где nu - коэффициент обучения.
Увеличить k на 1 и перейти к п. 2.

Представленный алгоритм работает в режиме "оффлайн", принимая обучающие пары <x^k, d^k> и оперативно корректируя значения весов.

Сети RMLP широко используются для построения формальных математических моделей реальных динамических объектов, для чего используется следующая схема обучения.

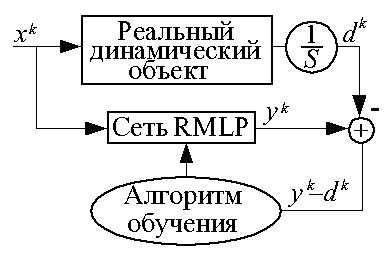
Деление выходного сигнала реального объекта на масштабный коэффициент S необходимо для приведения диапазона изменения этого сигнала к диапазону выходного сигнала сети -1...1 (при использовании биполярной сигмоидальной функции активации).

Обученная по такой схеме сеть RMLP может использоваться, например, в численных экспериментах по отработке алгоритмов управления динамическим объектом.

Рекуррентная сеть Эльмана

Сеть данного типа характеризуется частичной рекуррентностью, в ней обратной связью с единичной задержкой охвачен только первый слой нейронов. Структурная схема сети представлена ниже.

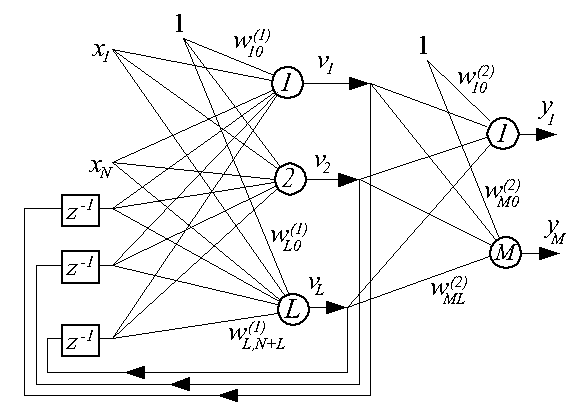
Здесь v_l, l=1, 2, ..., L - выходные сигналы первого слоя. Вектор возмущения для момента k имеет следующий вид:

X^k=[1, x^k₁, x^k₂, ...,x^k_N, v^k-1₁, v^k-1₂, ...,v^k-1_L]^T.

Для нейронов первого слоя

u^k_l=sum[j=0:N+L](w⁽¹⁾_lj*x^k_j), v^k_l=f₁(u^k_l).

Для нейронов выходного слоя

g^k_i=sum[l=0:L](w⁽²⁾_il*v^k_l), y^k_i=f₂(g^k_i).

Целевая функция имеет стандартный вид

E^k(W)=(1/2)*sum[i=1:M]((y^k_i-d^k_i)²)=(1/2)*sum[i=1:M]((e^k_i)²).

Получим выражения для частных производных целевой функции по весовым коэффициентам, необходимые для обучения сети методом градиента. Начнем с выходного слоя.

дE^k(W)/дw⁽²⁾_nm = sum[i=1:M](e^k_i*df₂(g^k_i)/dg^k_i*dg^k_i/dw⁽²⁾_nm)
= sum[i=1:M](e^k_i*df₂(g^k_i)/dg^k_i*sum[l=0:L](d(w⁽²⁾_il*v^k_l)/dw⁽²⁾_nm))
= sum[i=1:M](e^k_i*df₂(g^k_i)/dg^k_i*sum[l=0:L](dv^k_l/dw⁽²⁾_nm*w⁽²⁾_il+dw⁽²⁾_il/dw⁽²⁾_nm*v^k_l)).

Поскольку в сети Эльмана обратных связей с выходного слоя нет, то dv^k_l/dw⁽²⁾_nm=0 и выражение упрощается.

дE^k(W)/дw⁽²⁾_nm = sum[i=1:M](e^k_i*df₂(g^k_i)/dg^k_i*sum[l=0:L](dw⁽²⁾_il/dw⁽²⁾_nm*v^k_l)).

С учетом того, производная dw⁽²⁾_il/dw⁽²⁾_nm равна 1 при n=i и m=l, и равна 0 при всех остальных сочетаниях значений i и l, в итоге имеем

дE^k(W)/дw⁽²⁾_nm=e^k_n*df₂(g^k_n)/dg^k_n*v^k_m.

Кстати, легко заметить, что это выражение повторяет формулу расчета производной в методе обратного распространения ошибки для выходного слоя многослойного персептрона. Это так и должно быть, т.к. в сети Эльмана последний слой нейронов обратными связями не охвачен.

Вывод выражений для производных целевой функции по весам нейронов первого слоя более громоздок.

дE^k(W)/дw⁽¹⁾_nm = sum[i=1:M](e^k_i*df₂(g^k_i)/dg^k_i*sum[l=0:L](d(w⁽²⁾_il*v^k_l)/dw⁽¹⁾_nm)) = sum[i=1:M](e^k_i*df₂(g^k_i)/dg^k_i*sum[l=0:L](w⁽²⁾_il*dv^k_l/dw⁽¹⁾_nm)).

Отдельно определим

dv^k_l/w⁽¹⁾_nm = df₁(u^k_l)/du^k_l*sum[j=0:N+L](d(w⁽¹⁾_lj*x^k_j)/dw⁽¹⁾_nm)
= df₁(u^k_l)/du^k_l*sum[j=0:N+L](dw⁽¹⁾_lj/dw⁽¹⁾_nm*x^k_j+dx^k_j/dw⁽¹⁾_nm*w⁽¹⁾_lj).

Поскольку производная dw⁽¹⁾_lj/dw⁽¹⁾_nm равна 1 при l=n и j=m, а при всех остальных сочетаниях l и j равна 0, то заменим ее дельтой Кронекера deltha_ln, а произведение deltha_ln*x^k_m вынесем из под знака суммирования.

dv^k_l/dw⁽¹⁾_nm = df₁(u^k_l)/du^k_l*(deltha_ln*x^k_m+sum[j=0:N+L](dx^k_j/dw⁽¹⁾_nm*w⁽¹⁾_lj)).

Поскольку во входном векторе сети зависимыми от весов первого слоя нейронов являются только последние L компонент в итоге имеем:

dv^k_l/dw⁽¹⁾_nm = df₁(u^k_l)/du^k_l*(deltha_ln*x^k_m+sum[j=1:L](dv^k-1_j/dw⁽¹⁾_nm*w⁽¹⁾_l,N+j)).

Начальные значения производных для момента k=0 принято выбирать нулевыми.

Алгоритм обучения сети Эльмана можно представить в следующем виде.

Присвоить весам начальные значения, положить k=1.
Для текущего момента k определить все сигналы сети.
Рассчитать значения dv^k_l/dw⁽¹⁾_nm для всех весов нейронов первого слоя.
Рассчитать все компоненты вектора градиента целевой функции.
Скорректировать веса нейронов обоих слоев по формулам:

w⁽²⁾_nm<-w⁽²⁾_nm-nu*дE^k(W)/дw⁽²⁾_nm,
w⁽¹⁾_nm<-w⁽¹⁾_nm-nu*дE^k(W)/дw⁽¹⁾_nm,

Увеличить k на 1 и перейти к п. 2.